物体在倾斜的表面上的运动
1。物体以沿倾斜表面恒定速度滑动的条件
如图1所示,一个物体可以通过将倾斜角度θ的倾斜表面放在恒定速度下滑动。尝试在倾斜的表面和对象之间找到动态摩擦因子。
应力分析如图2所示,从平衡条件下,我们可以获得:

F-MGSINθ= 0
N-MGCOSθ= 0
f =μn
从以上三个公式中,我们可以获得:μ=tanθ
2。当一个物体可以沿着倾斜的表面恒定速度滑动时,它与物体的质量无关。
如果m(与M相同的材料)放置在上面提到的斜率上,则对象M仍能以恒定的速度滑动?
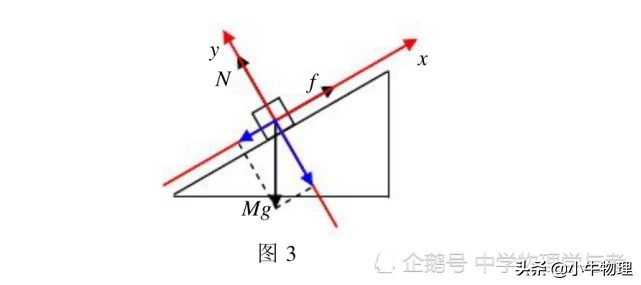
如图3所示,M在垂直于倾斜表面的方向上进行分析力。
n =mgcosθ
根据滑动摩擦法,我们可以知道:
f =μn=μmgcosθ=mgtancosθ=mgsinθ
它正是沿坡度向下的重力摩擦。这意味着对象M可以沿倾斜平面恒定速度移动。
同时,以上讨论说明了一个问题:如果对象可以在倾斜的表面上以均匀的速度滑动,则在增加对象的质量后,物体可以在倾斜的表面上以均匀的速度滑动。物体可以沿着倾斜的表面滑动与物体的质量无关。
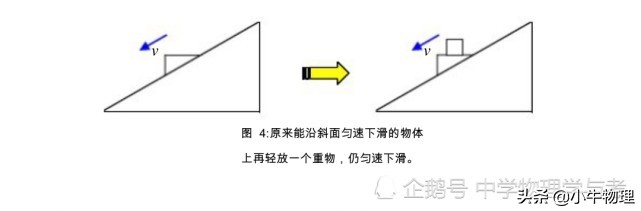
3。将垂直向下力施加到最初以恒定速度向下滑动的物体,并且对象仍然可以以恒定的速度滑动。
如图5所示
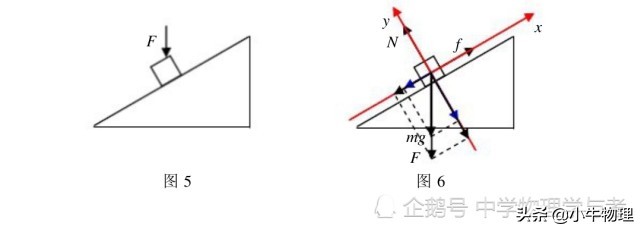
如图所示,将垂直向下力f应用于最初以恒定速度滑动以讨论对象运动的对象。如图6所示,对象经过应力分析。在垂直方向上,可以获得平衡条件:
n =(mg + f)cosθ

根据滑动摩擦法,我们可以知道:
f = un =(mg f)tancosθ=(mg f)sinθ
它完全等于沿倾斜表面的重力和力F向下的联合力,因此物体可以沿着倾斜的表面恒定速度向下滑动。
4。增加对象的质量并在对象上施加垂直向下力不会改变对象的运动状态。
对以下三个练习有一个统一的解决方案:
(1)如图7所示
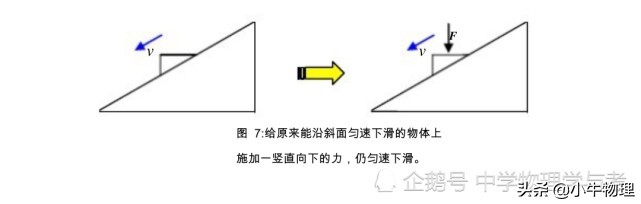
如图所示,众所周知,倾斜角为θ,使对象沿倾斜度向下向下速度,并且物体可以沿倾斜度均匀的速度向下滑动。尝试在倾斜的表面和对象之间找到动态摩擦因子。
(2)如图4的右图所示,众所周知,倾斜度的倾斜角为θ,一个对象按在另一个对象上,使整个对象沿着倾斜度向下向下下降,并且整个物体可以沿着倾斜度均匀地向下滑动。尝试在倾斜的表面和对象之间找到动态摩擦因子。
(3)如图5所示,众所周知,倾斜度的倾斜角为θ,并且将垂直向下的恒定力F施加到对象上,以便对象可以沿着倾斜度恒定速度向下滑动。尝试找到对象和倾斜表面之间的动态摩擦因子。
如图8所示
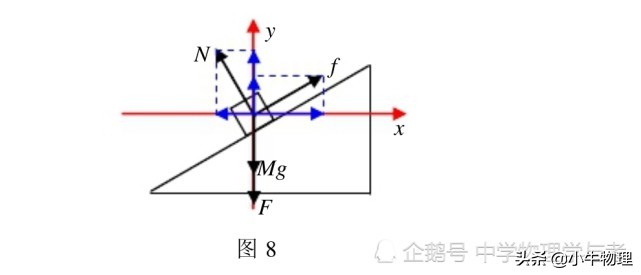
建立一个笛卡尔坐标系,可以从平衡条件下沿x轴方向看出:
fcosθ-nsinθ= 0
那就是:f/n =sinθ/cosθ=tanθ
根据滑动摩擦法,我们可以知道:
μ= f/n =tanθ
上面的解决方案仅使用水平平衡方程和滑动摩擦定律,并且不涉及垂直力。尽管N和F在这个问题中都是未知数,但对于这三个问题,N和F的幅度也有所不同,但它们的比率总是相同的。这也是动态摩擦因子与物体的质量无关的原因,而在这三种情况下,力f垂直向下应用。
5。在不等状态下,增加物体的质量并在对象上施加垂直向下力将不再等效。
从上面的讨论中,我们可以看到,当对象以恒定的速度向下滑动时,将质量添加到对象和向下施加向下力是相同的,并且对象仍然可以以恒定的速度以均匀的线性方式移动。这很容易导致一个错误的想法,即在任何情况下,质量增加等同于添加垂直向下力。但事实并非如此。查看以下两个问题。
(4)将物体放在倾斜的表面上,并用沿倾斜表面向下的加速度A进行均匀的加速运动。现在将另一个重物放在这个对象上。尝试判断对象的加速度将如何变化。
(5)将物体放在倾斜的表面上,并用沿倾斜表面向下的加速度A进行均匀的加速运动。现在,将另一个垂直向下力f应用于此对象。尝试判断对象的加速度将如何变化。
[解决方案]:(4)如图3所示,可以从牛顿的第二定律中看出:
mgsinθ-f = ma
N-MGCOSθ= 0

根据滑动摩擦法,我们可以知道:
f =μn
从上面的三个公式中,您可以得到:
a = g(sinθ-μcosθ)
该结果表明,向下滑动时对象的加速与质量无关。因此,当对象的质量增加时,对象的加速不会改变。
(5)如图6所示,可以从牛顿的第二定律中获得:
(mg + f)sinθ-f = ma
n-(mg + f)cosθ= 0
根据滑动摩擦法,我们可以知道:
f =μn
从上面的三个公式中,您可以得到:
a =(g+f/m)(sinθ-μcosθ)
这表明对象的加速度与垂直向下施加的力f有关,并且可以看出,对象的加速度在添加力F后将增加。
通过比较上面的两个练习,我们发现当对象加速并向下滑动时,将质量添加到对象并将垂直向下力施加到对象上将不再等效。
我们可以通过综合方程式更清楚地看到这一点:
(M+M)GSINθ-μ(M+M)GCOSθ=(M+M)a
该方程式的两侧都有一个共同的因子M+M,因此M是否等于0(即增加质量,如果不增加质量)不会改变对象的加速度。对象平衡和不平衡都没有以此为特征。
(mg + f)sinθ-μ(mg + f)cosθ= ma
当a = 0时,您会看到添加了力f,并且对象的平衡状态不会更改。
当A≠0时,添加力F等于更改方程式的左侧,右侧的M保持不变,因此加速度A必须更改。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请联系本站,一经查实,本站将立刻删除。如若转载,请注明出处:https://www.jinboyatc.com/html/tiyuwenda/7543.html






