对于扁平运动,治疗方法通常是正交分解,坐标系通常是水平和垂直矩形坐标系。实际上,矩形坐标系统的建立是任意的,并且根据解决问题的需求建立。可以沿着倾斜的表面建立扁平运动和倾斜表面的组合。
除了正交分解的加工方法外,它还可以倾斜分解。实际上,没有固定的分解模式,并且可以根据解决问题的需求有多种分解方法。
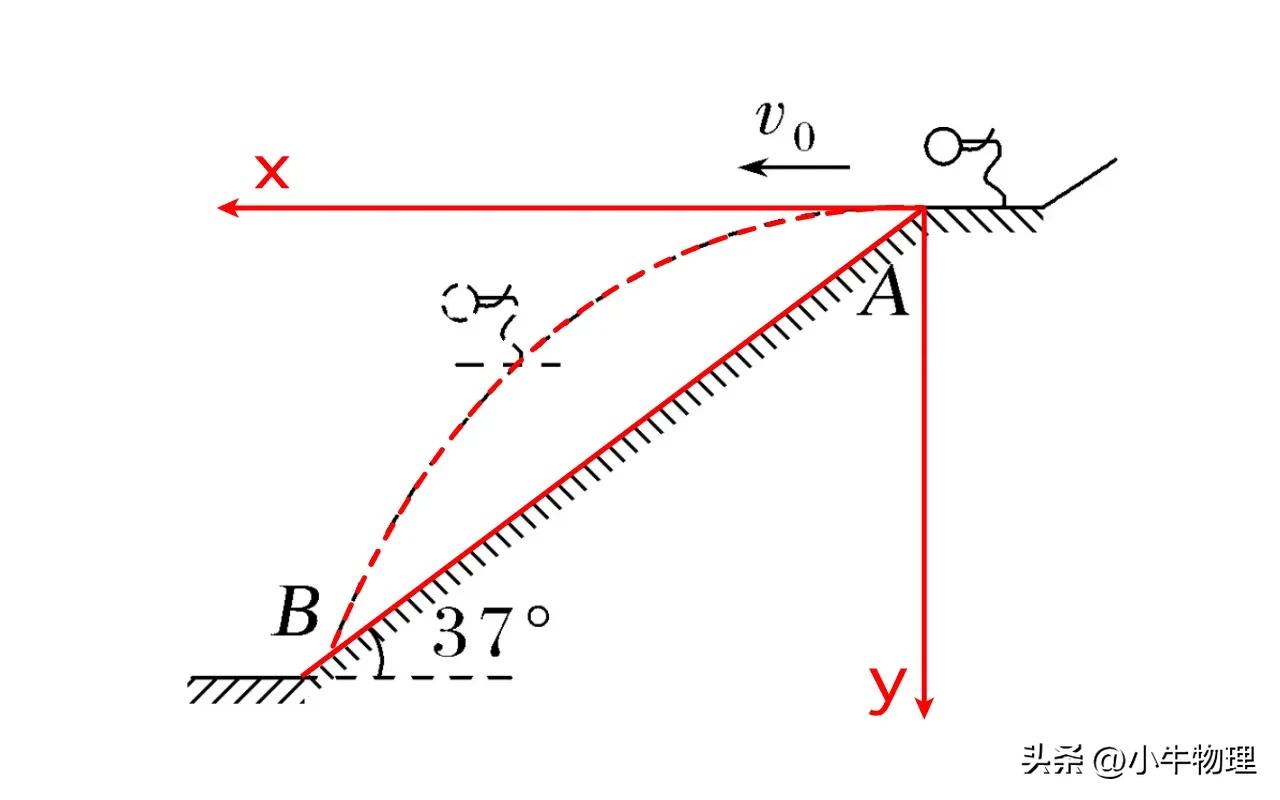
示例:如图所示,
一个女性滑雪跳线踩在一个没有雪球的特殊滑雪板上,在辅助轨道上速度(未绘制),水平飞出,在降落前飞往空中距离。假设运动员从斜坡顶部的A上飞出的速度为v₀= 20 m/s,着陆点是斜坡上的点B,坡度倾斜角θ= 37°,无论空气阻力,坡度都可以视为倾斜的表面(无论是g = 10 m/s 2,sin37°= 0.6°= 0.6,cos37°= 0.8)。求:
(1)运动员在空中飞行的时间;
起点和着陆点在同一倾斜平面上,位移偏转角为θ,tanθ= y/x = gt/2v₀,t =2v₀tanθ/g。
(2)A和B之间的距离;

x =v₀t=2v₀²tanθ/g
s = x/cosθ=v₀t/cosθ
(3)运动员降落在倾斜表面时的速度;
(4)运动员何时离斜坡最远?
距倾斜平面最远的速度是平行于倾斜平面的,即速度偏转角为θ,tanθ= gt/v₀,t =v₀tanθ/g。
距离某个平面最远的速度与该平面平行。
(5)从运动员到倾斜表面的最远距离。
方法1:正交分解方法
沿水平和垂直方向建立矩形坐标系,并使用速度反向扩展线在水平位移的中点相交。
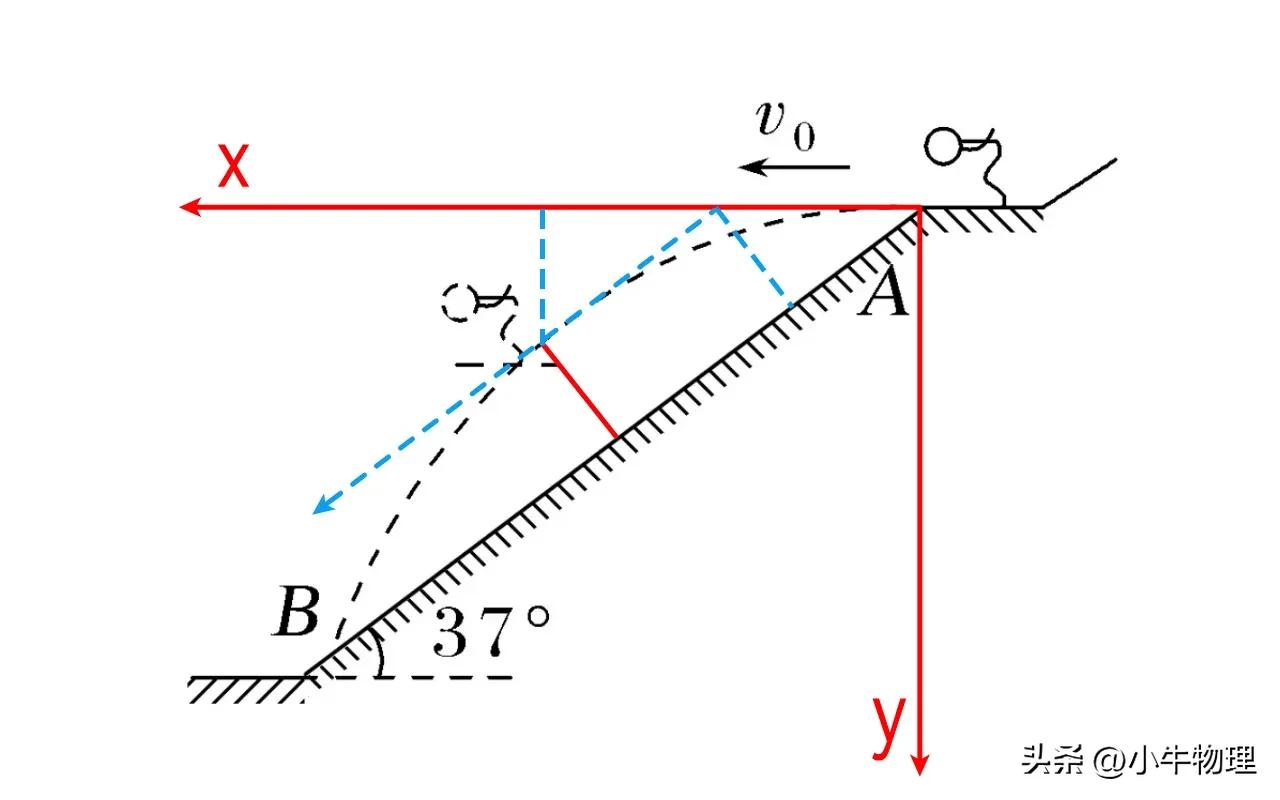

运动描述:沿水平方向恒定线性运动,并在垂直方向上进行自由秋季运动。
速度反向扩展线在水平位移的中点相交。
dm =xsinθ/2 =v₀tsinθ/2
=v₀²sin²θ/2gcosθ
方法2:正交分解方法
沿着倾斜和垂直的倾斜平面建立矩形坐标系。
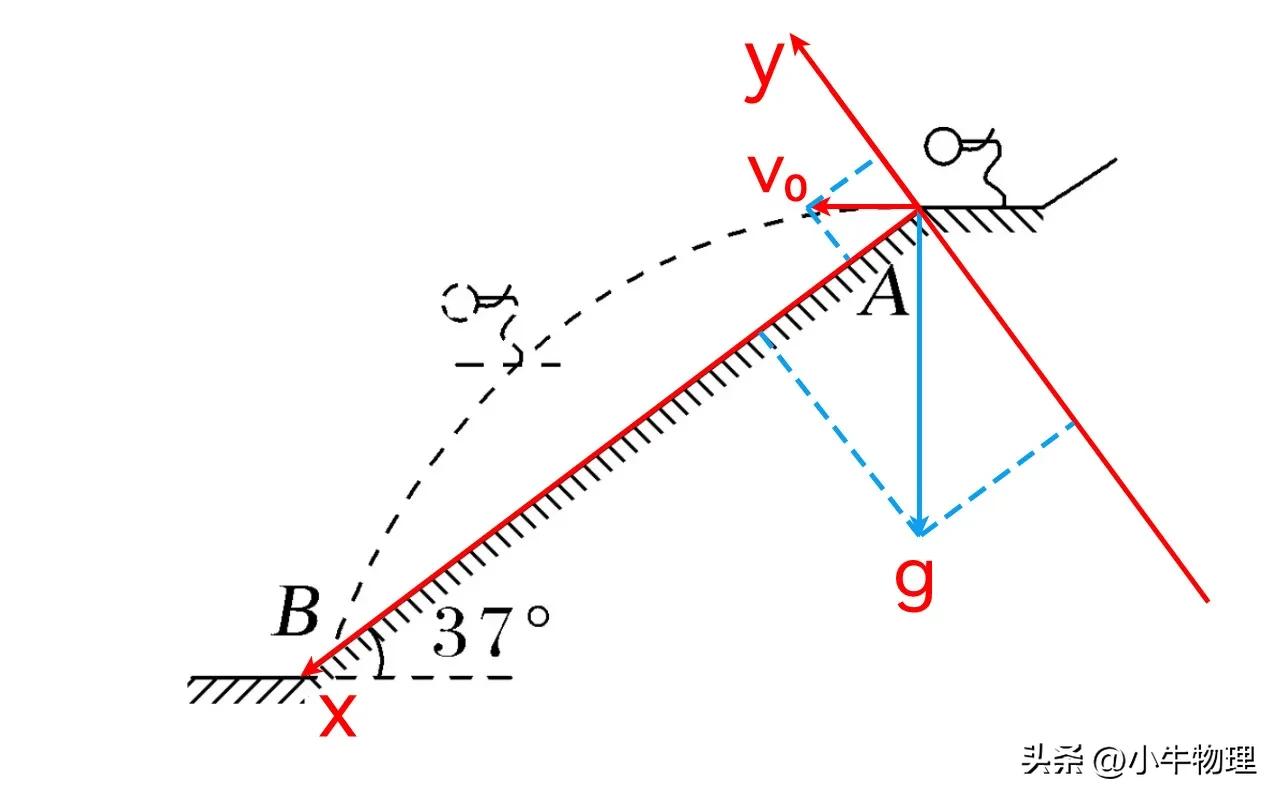
运动描述:
X轴:具有初始速度V₀Cosθ和加速度GSINθ(例如垂直向下运动)的均匀加速线性运动。
Y轴:首先,使用初始速度V₀sinθ和加速度GCOSθ执行均匀的减速线性运动,然后在逆转的加速度GCOSθ进行均匀的加速度运动(例如垂直向上投掷运动)。
当Y轴速度为零时,它离倾斜度最远。
dm =(v₀sinθ)²/2gcosθ(将垂直向上投掷运动公式)
方法3:对角线分解
沿着倾斜和初始速度方向建立X轴和Y轴。
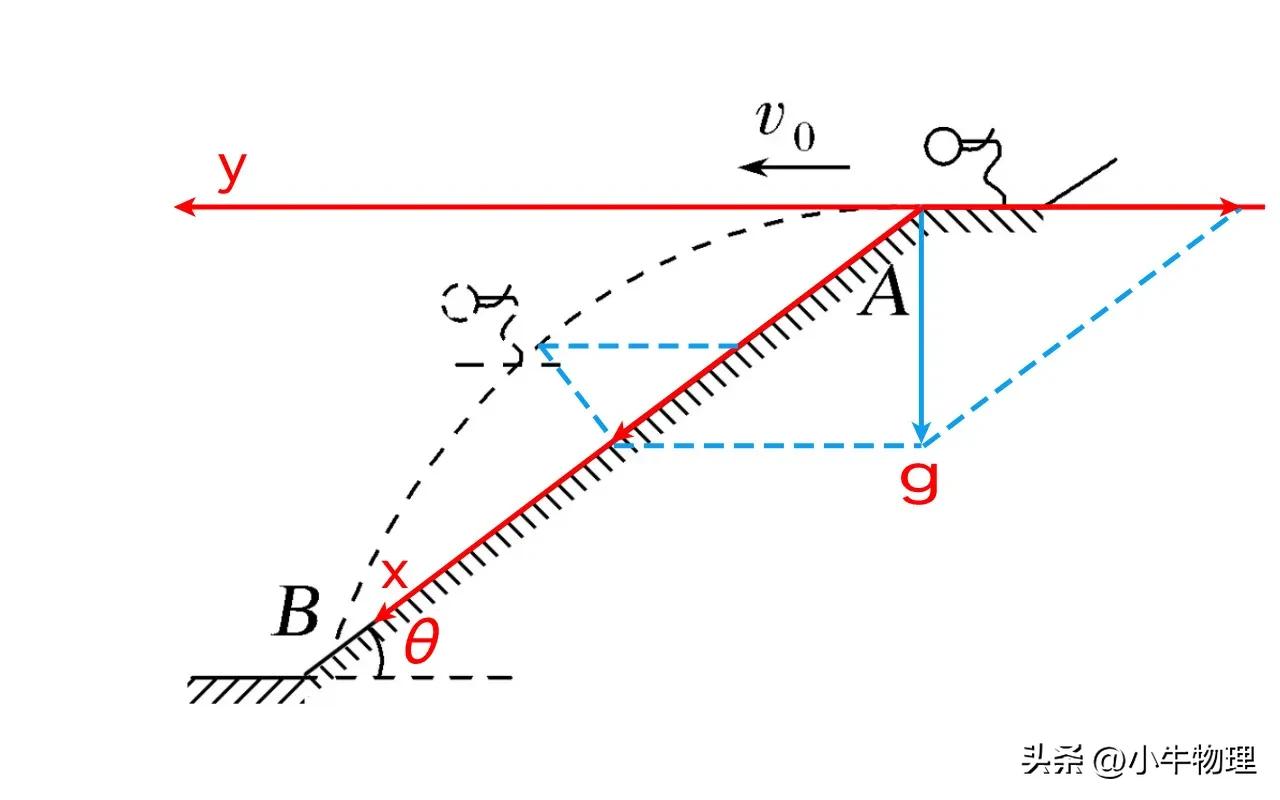
运动描述:
X轴:均匀的加速度线性运动,初始速度为零和加速度G/SINθ。
Y轴:如果初始速度为v₀,并且加速度为g/tanθ,则首先将线性运动统一减速,然后线性运动反向加速(例如垂直向上抛弃运动)。
当Y轴速度为零时,它离X轴最远。

t =v₀/g/tanθ=v₀tanθ/g。
y =v₀²/2/g/tanθ。
dm =ysinθ=v₀²sin²θ/2gcosθ。
方法4:对角线分解
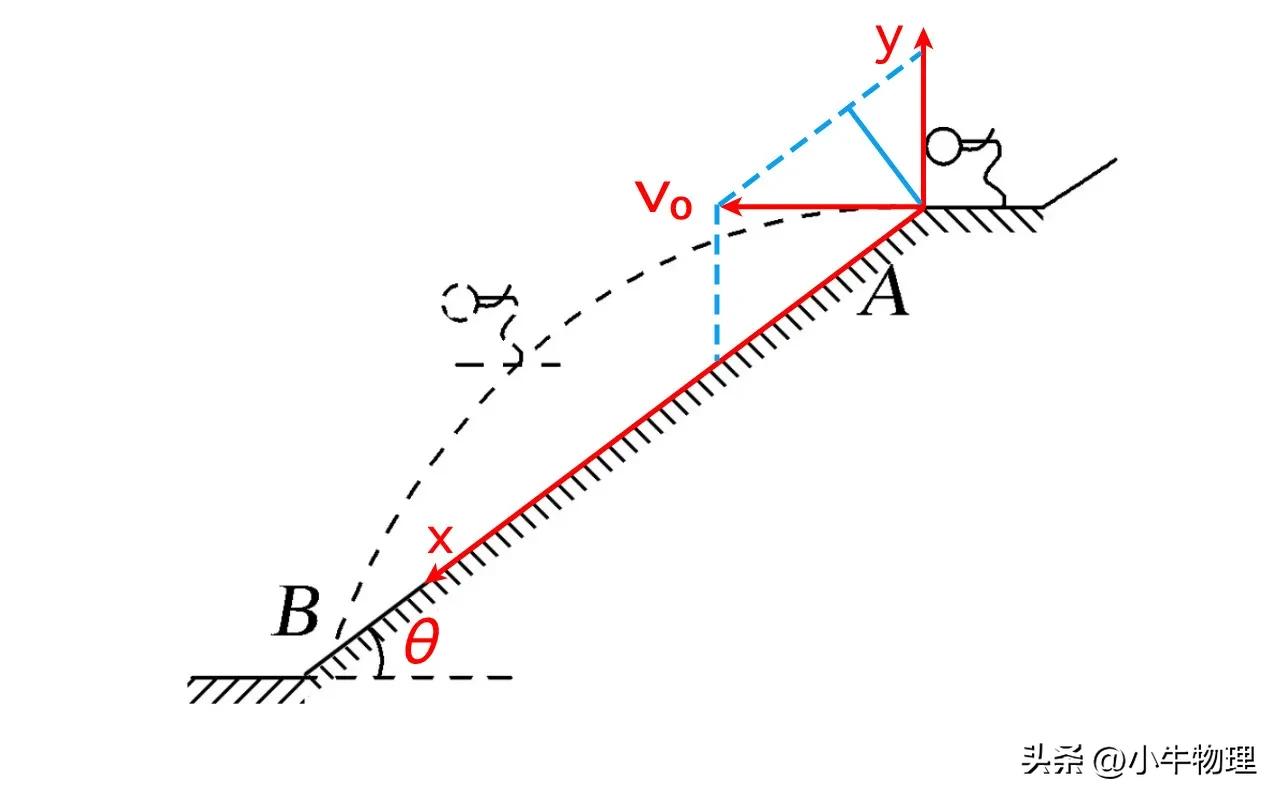
X轴:以V₀的恒定速度进行线性运动。
Y轴:以初始速度v₀tanθ和加速度g进行垂直向上投掷运动。
当y轴速度为零时,离x轴最远
y =v₀²tan²θ/2g。
dm =ycosθ=v₀²sin²θ/2gcosθ。
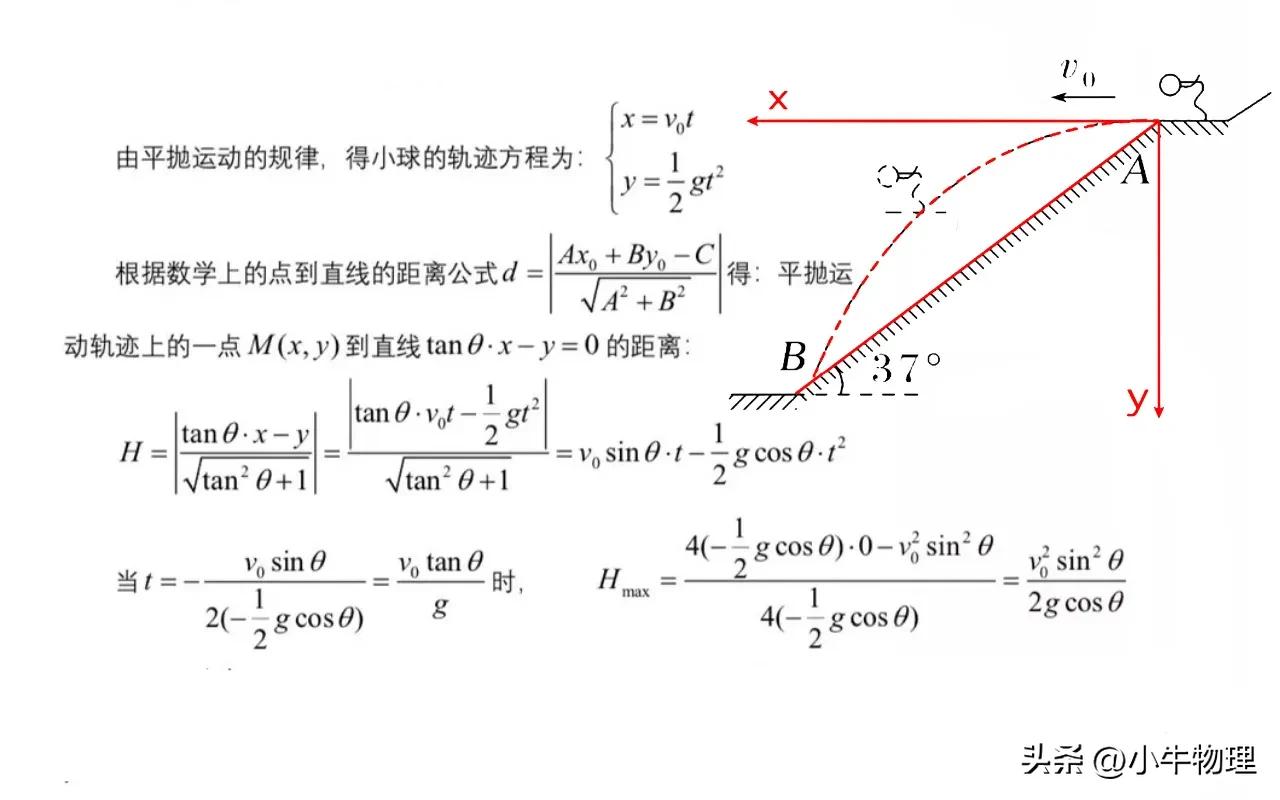
方法5:数学方法
数学知识:从一点点到直线的距离

扁平运动轨迹是抛物线,方程为y =gx²/2v₀²。倾斜的表面是一条直线,方程为y =tanθ·x。
总而言之:对于倾斜运动,可以在正交或倾斜上分解。坐标系选择也是任意的。必须根据解决问题的需求选择适当的坐标系。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请联系本站,一经查实,本站将立刻删除。如若转载,请注明出处:https://www.jinboyatc.com/html/tiyuwenda/7547.html






